Total driving time =24
Mom drove =75 mile per hours
Dad drove = 60 miles per hours
Total distance =1710
Let

Total time:

Formula:
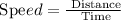
For Ava's mom:
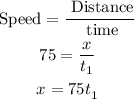
For Ava's dad:

Put the value of "x" then:
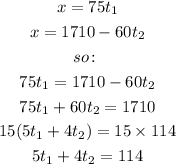
Solve the both eq then:
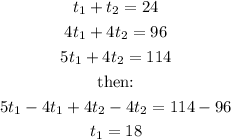
So Ava's mom drive 18 hours
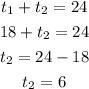
Ava's dad driving 6 houras