To answer this question, we need to use the next formula for compound interest:
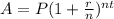
From the formula, we have:
• A is the accrued amount. In this case, A = $7900.
,
• P is the principal amount. In this case, $4500.
,
• r is the interest rate. In this case, we have 4.7%. We know that this is equivalent to 4.7/100.
,
• n is the number of times per year compounded. In this case, we have that n = 365, since the amount is compounded daily.
Now, we can substitute each of the corresponding values into the formula as follows:
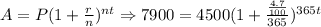
And we need to solve for t to find the number of years, as follows:
1. Divide both sides by 4500:
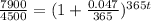
2. Applying natural logarithms to both sides (we can also apply common logarithms):
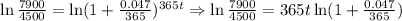
3. Then, we have:
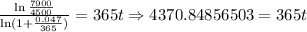
4. And now, we have to divide both sides by 365:

If we round the answer to two decimals, we have that t is equal to 11.97 years.