Answer:
Slope -intercept for of equation 1:
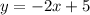
Slope -intercept for of equation 2:

Looking at slope-intercept form of both equations, we have slope m = -2
Both have same slopes so, the lines are parallel.
Explanation:
We need to write equations in slope-intercept form.
The general formula of slope-intercept form is:
 where m is slope and b is y-intercept.
where m is slope and b is y-intercept.
The first equation is:

Slope-intercept form:
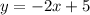
The second equation is:
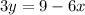
Rearranging:

Slope-intercept form:

Slope -intercept for of equation 1:
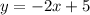
Slope -intercept for of equation 2:

Looking at slope-intercept form of both equations, we have slope m = -2
Both have same slopes so, the lines are parallel.
They have different y-intercepts.