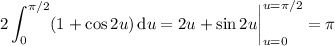Recall that a circle of radius 2 centered at the origin has equation
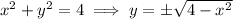
where the positive root gives the top half of the circle in the x-y plane. The definite integral corresponds to the area of the right half of this top half. Since the area of a circle with radius

is
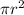
, it follows that the area of a quarter-circle would be

.
You have
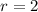
, so the definite integral is equal to
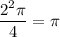
.
Another way to verify this is to actually compute the integral. Let

, so that
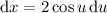
. Now
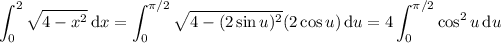
Recall the half-angle identity for cosine:
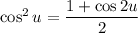
This means the integral is equivalent to