Question

Use technology or a z-distribution table to find the indicated area. Scores on a standardized military exam are normally distributed with a mean of 57 and a standard deviation of 9. Consider a group of 4000 military students. Approximately how many students will score less than 66 on the test?

200
634
3366
3800

Answer 1

Let
`X` denote the random variable for scores on the exam.
`X` is normally distributed with mean 57 and standard deviation 9. Let
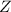
`Z` denote the random variable for scores following the standard normal distribution.

You have


`\mathbb P(X<66)=\mathbb P\left(\frac{X-57}9<\frac{66-57}9\right)=\mathbb P(Z<1)`

You could use a table of z-scores to get a precise answer, or you could apply the empirical rule. You know 100% of the scores are contained within the distribution. The empirical rule states that approximately 68% of them will fall within one standard deviation of the mean, which means 32% fall without, with 16% lying to either side of this range.


`\underbrace{100\%}_{\text{total}}=\underbrace{16\%}_(Z<-1)+\underbrace{68\%}_(-1<Z<1)+\underbrace{16\%}_(Z>1)`


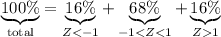
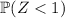
`\mathbb P(Z<1)` corresponds to the first two ranges, i.e.


`\mathbb P(Z<1)=\mathbb P(Z<-1)+\mathbb P(-1<Z<1)=16\%+68\%=84\%`

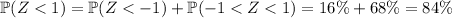
So out of 4000 students, you can expect 84% of them, or about 3360, to score lower than a 66. This means the answer is 3366.

More precisely,
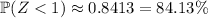
`\mathbb P(Z<1)\approx0.8413=84.13\%`, which means closer to 3366 students would fall in this range.