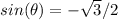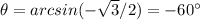Answer:
Part 1) option a

Part 2)
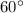
Part 3)

Explanation:
Part 1) Which expression represents θ in terms of x?
we have

so
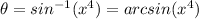
Part 2) What is the value of arcsin(√3/2) in degrees?
Let
 ----> the angle
----> the angle
we know that
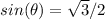
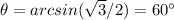
Part 3) What is the value of arcsin(-√3/2) in degrees?
Let
 ----> the angle
----> the angle
we know that