Question

Find the area of the

regular figure below:

A) 466 mm2
B) 430 mm2
C) 404 mm2
D) 495 mm2
E) 512 mm2

explain pls

Answer 1

Option A

Explanation:

Central angle of the pentagon =
`\frac{360}{\text{Number of sides of the regular polygon}}`

=
`(360)/(5)`

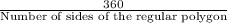
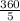
= 72°

Measure of ∠BAC = 72°

Therefore, measure of ∠BAD =
`(72)/(2)`

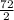
= 36°

By sine rule in ΔABD,

sin(36°) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

=
`(BD)/(AB)`

=
`(BD)/(14)`

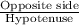
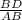
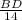
BD = 14(sin36°)

= 8.23 mm

Similarly, by cosine rule,

cos(36°) =
`\frac{\text{Adjacent side}}{\text{Hypotenuse}}`

=
`(AD)/(AB)`

=
`(AD)/(14)`

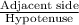
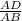
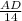
AD = 14(cos36°)

= 11.33 mm

Area of ΔABC = 2(Area of ΔABD)

=
`2((1)/(2)(\text{Base})(\text{Height})`

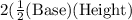
= AD × BD

= 11.33 × 8.23

= 93.21 mm²

Since, area of regular pentagon given in the picture = 5(area of ΔABC)

= 5(93.21)

= 466 mm²

Therefore, Option A will be the answer.