Question

Find the area of the

regular figure below:

A) 67.3 in2
B) 70.2 in2
C) 74.6 in2
D) 77.1 in 2
E) 82.8 in2

pls show work

Answer 1

Option E

Explanation:

Central angles of a regular polygon =
`(360)/(n)`

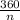
Here, n = Number of sides of the regular polygon

Therefore, central angle of the regular polygon =
`(360)/(8)` = 45°

From the picture attached,

m∠AOB =
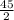`(45)/(2)` = 22.5°

By tangent rule,

tan(∠AOB) =
`\frac{\text{Opposite side}}{\text{Adjacent side}}`

tan(22.5°) =
`(AB)/(OB)`

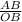
AB = OB[tan(22.5°)]

AB = 5(0.414213)

= 2.07 in

Therefore, area of ΔAOC = 2 × (Area of ΔABO)

=
`2((1)/(2))(\text{Base})(\text{Height})`

= AB × OB

= 2.07 × 5

= 10.35 in²

Since, area of the given regular octagon = 8 × (Area of ΔAOC)

= 8(10.35)

= 82.5 in²

Therefore, Option (E) is the answer.