ANSWER
x = 10.2
Step-by-step explanation
In this problem, we are given a right triangle: one of its non-right interior angles measures 22°. We know that the length of the hypotenuse is 11 units long and we have to find the length of the side adjacent to the given angle, x.
With the given information, we can use the cosine of the angle to find the missing value,
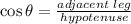
In this problem,
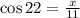
Solving for x,
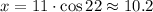
Hence, the value of x is 10.2, rounded to the nearest tenth.