Question

Suppose you're flying a kite, and it gets caught at the top of the tree. You've let out all 100 feet of string for the kite, and the angle that the string makes with the ground is 75 degrees. Instead of worrying about how to get your kite back, you wonder. How tall is that tree?

Answer 1

check the picture below

recall your SOH CAH TOA


`\bf in(\theta)=\cfrac{opposite}{hypotenuse} \qquad \qquad % cosine cos(\theta)=\cfrac{adjacent}{hypotenuse} \\ \quad \\ % tangent tan(\theta)=\cfrac{opposite}{adjacent}`

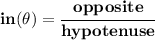
we have,
the angle,
the hypotenuse,
we want the opposite side

which of those fellows have only that? ahhhh it has to be Ms Sine,
so let's ask her

`\bf sin(\theta)=\cfrac{opposite}{hypotenuse}\implies sin(75^o)=\cfrac{x}{100}\implies 100\cdot sin(75^o)=x`

the opposite side "x", is how tall the tree is

when taking the sine function, make sure your calculator is in Degree mode, since the angle is in degrees

Answer 2

The answer to your problem is x= 96.6 ft