Question

between 1995 and 2006, the population of samburg, usa(in thousands) can be modeled by f(x) = 0.35x(squared) - 2.1x+15.8 where x=0 represents 1995. Based on this model, in what year did the population of samburg reached it's minimum?

Answer 1

`\bf f(x)=0.35x^2-2.1x+15.8\qquad \begin{cases} x=\textit{year since 1995}\\ f(x)=\textit{population amount} \end{cases}`

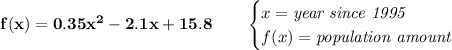
the equation is a quadratic one, and it has a positive coefficient on the leading term, meaning, is opening upwards, so it has a "burrow" for the vertex.

the minimum or lowest point for a quadratic opening upwards is, well, the vertex point :), the "x" value is the year, the "y" or f(x) value is the population, we're asked for the year, or the x-coordinate of the vertex

well
`\bf \begin{array}{llll} f(x)=&0.35x^2&-2.1x&+15.8\\ &\quad \uparrow &\quad \uparrow&\uparrow \\ &\quad a&\quad b &c \end{array} \\\\ \\\\ \qquad \textit{vertex of a parabola}\\ \quad \\ \qquad \left(\boxed{-\cfrac{{{ b}}}{2{{ a}}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right)`