Question

Given that OP is the perpendicular bisector of MN, which segments are congruent?

Answer 1

whats the options...

Answer 2

Explanation:

Let OP be perpendicular bisector of MN

Perpendicular:

We say two lines are perpendicular to each other if they intersect at right angle.

If OP is perpendicular to MN at point say K , it means
`\angle OKN=90^(\circ)`

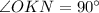
Bisector:

A line is said to be a bisector of another line if it intersects that line at it's midpoint .

If OP bisects MN at point K, it means MK=KN

Two line segments are said to be congruent if they are of same length.

Join OM and ON

Consider
`\Delta OKM \,,\,\Delta OKN`

OK=OK (common side)

MK=KN (OP bisects MN)

`\angle OKM =\angle  OKN`
`\left ( OP\perp MN \right )`

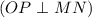
Therefore, ΔOKM≅ΔOKN ( by SAS congruence condition )

So, OM=ON ( corresponding sides of congruent triangles )