Question

A code is made up of 1 letter, out of a possible 26, in the first position. One digit, 0–9, occupies each of the second and third positions. The digit cannot be repeated. How many possible outcomes exist?

Answer 1

26 possibilities for the first location,
10 possibilities for the next location,
9 possibilities for the last location (because we've used a number in the previous slot and we're not allowed to repeat it).

26 x 10 x 9

Answer 2

Total number of possible ways to form the code is 2340.

Step-by-step explanation:

We have to make a code of 3 places.

First position occupied by any alphabet. Total number of alphabets is 26, therefore total number of possible ways to fill first place is 26.

Second and third positions must be occupied by any digit but repetitions of digits are not allowed.

Total number of digits is 10, therefore total number of possible ways to fill second place is 10.

Since second place occupied by a digit, therefore the number of remaining digits is 9 and total number of possible ways to fill third place is 9.

Total possibilities to form the code is

`T=26* 10* 9=2340`

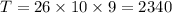
Therefore total number of possible ways to form the code is 2340.