Question

Two cars travel in the same direction along a straight highway, one at a constant speed of 55 mi/h and the other at 60 mi/h.(a) Assuming they start at the same point, how much sooner does the faster car arrive at a destination 14 mi away?_____ min(b) How far must the faster car travel before it has a 15-min lead on the slower car?_____ mi

Answer 1

We will have the following:

a) We first determine the time it takes to travel the distance to both vehicles:

*

`t_1=(14mi\ast1h)/(55)\Rightarrow t_1=(14)/(55)h`

*

`t_2=(14mi\ast1h)/(60mi)\Rightarrow t_2=(11)/(12)h`

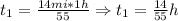
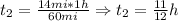
So, we determine now the difference in time:

`(11)/(12)h-(14)/(55)h=(437)/(660)h\approx0.66h`

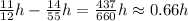
So, the fastest car will arrive approximately 0.66 hours sooner.

b) We determmine the distance it must travel the fastest car to have a 15 minute lead on the other one as follows:

First, we determine the time difference required:

`t=(15min\ast1h)/(60min)\Rightarrow t=0.25h`

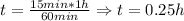
Then, since both vehicles will move relative to each other, we will have that:

`d_(c1)=(60mi/h)(0.25h)\Rightarrow d_(c1)=15mi`

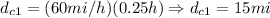
So, the fastest car must be 15 miles ahead of the other car in order to have a 15 minute lead with respect to the second car.