Question

c) Suppose that you take a random sample of 5,000 people from the U.S. population.Make a table that shows the expected number of people in your sample who come fromeach of the four age groups

Answer 1

In order to determine the number of people in the sample for each age group, here are the steps:

1. Determine what proportion in the entire population the population of each group. To get the proportion, simply divide the population of each respective group by the entire population.

2. To get the number of samples for each group, multiply the proportion by 5,000 and round the answer to the nearest whole number.

Now, let's apply the steps above in each group.

Let's start with ages under 18.

`\begin{gathered} Proportion:74,181,467/308,745,538=0.240267333 \\ Number\text{ }of\text{ }Samples:0.240267333*5,000=1,201.33\approx1,201 \end{gathered}`

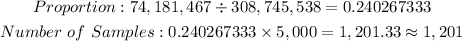
Hence, we are expected to have 1,201 people aged under 18 in the sample.

For those aged 18 - 44,

`\begin{gathered} Proport\imaginaryI on:112,806,642/308,745,538=0.3653709224 \\ Number\text{ }of\text{ }Samples:0.3653709224*5,000=1,826.85\approx1,827 \end{gathered}`

Hence, we are expected to have 1,827 people aged 18-44 in the sample.

For those aged 45 - 64,

`\begin{gathered} Proportion:81,489,445/308,745,538=0.2639372395 \\ Number\text{ }of\text{ }Samples:0.2639372395*5,000=1,319.68\approx1,320 \end{gathered}`

The expected number of samples for people aged 45-64 is 1,320.

Lastly, for aged 65 and over,

`\begin{gathered} Proportion:40,267,984/308,745,538=0.1304245051 \\ Number\text{ }of\text{ }Samples:0.1304245051*5,000=652.12\approx652 \end{gathered}`

The expected number of samples for people aged 65 and over is 652.

To summarize, we have:

Age under 18 ⇒ 1,201 samples

18 - 44 ⇒ 1,827 samples

45 - 64 ⇒ 1,320 samples

65 and over ⇒ 652 samples

.