Question

You can model the population of a certain city between 1945-2000 by the radical function p(x)=55,000√x-1945. Using this model in which year was the population of that city 165,000?

Answer 1

165,000 = 55,000 sqrt x - 1945

find x:-

55000 sqrt x = 166945
sqrt x = 166945/55000 = 3.035

x = 9.2

so required year = 1945 + 9 = 1954

Answer 2

In 1954 the population of the city became 165,000.

Explanation:

Given : You can model the population of a certain city between 1945-2000 by the radical function
`p(x)=55,000√(x-1945)`

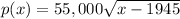
To find : Using this model in which year was the population of that city 165,000?

Solution : The model of the function is

`p(x)=55,000√(x-1945)`

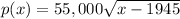
where p(x) is the population and x is the time (in years)

To find the year in which population reach 165,000

p(x)= 165,000, substitute the value in p(x)

`165000=55000√(x-1945)`

`(165000)/(55000)=√(x-1945)`

`3=√(x-1945)`

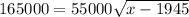
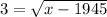
Squaring both side,

`3^2=(√(x-1945))^2`

`9=x-1945`

`x=1945+9`

`x=1954`

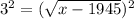
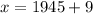
So, In 1954 the population of the city became 165,000.