Question

Find tan 19pi/12 using an angle addition and subtraction

Answer 1

(1+sqrt3)/(1-sqrt3)

Explanation:

Answer 2

We need to find a clever way to break up 19pi/12 into two different values. We want the two values to be special angles.

We want the two values to divide into 12 so we can simplify the fractions. One option is to break 19 into 4 and 15.


`\rm (19\pi)/(12)\quad=\quad (4\pi)/(12)+(15\pi)/(12)`

simplifying our fractions,


`\rm (19\pi)/(12)\quad=\quad (\pi)/(3)+(5\pi)/(4)`

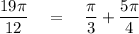
Apply your Tangent Angle Addition Identity,


`\rm \tan\left((19\pi)/(12)\right)=\tan\left((\pi)/(3)+(5\pi)/(4)\right)=(\tan(\pi)/(3)+\tan(5\pi)/(4))/(1-\tan(\pi)/(3)\tan(5\pi)/(4))`

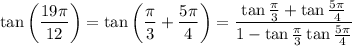
simplify each thing using your unit circle,


`\rm =(\sqrt3+1)/(1-√(3))`

multiply by conjugate of the denominator to rationalize,


`\rm =(1+\sqrt3)/(1-√(3))\left((1+\sqrt3)/(1+\sqrt3)\right)=((1+\sqrt3)^2)/(1-3)=((1+\sqrt3)^2)/(-2)`

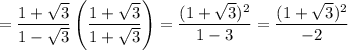
expanding the numerator,


`\rm =(1+2\sqrt3+3)/(-2)=(4+2\sqrt3)/(-2)`

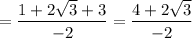
dividing each term by -2 as a final step,


`\rm =-2-\sqrt3`

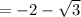
I hope that helps!