Question

Identify the 17th term of a geometric sequence where a1 = 16 and a5 = 150.06. Round the common ratio and 17th term to the nearest hundredth.

1.)a17 ≈ 123,802.31
2.)a17 ≈ 30,707.05
3.a17 ≈ 19,684.01
4.)a17 ≈ 216,654.05

Answer 1

The geometric sequence formula is expressed as an = a1 * r^(n-1) where n is an integer. In this case, upon substitution, 150.06 = 16 * r^(4). extracting r, r is equal to 1.75. Hence the 17th term from the formula is equal to 123802.32.

Answer 2

The correct option is 1.

Explanation:

It is given that the first term of a geometric sequence is 16 the fifth term of the sequence is 150.06.

`a_1=16`

`a_5=150.06`

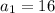
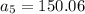
The nth term of a geometric sequence is

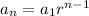`a_n=a_1r^(n-1)` .... (1)

The fifth term of the sequence is

`a_5=a_1r^(5-1)`

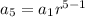
Substitute
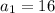`a_1=16` and
`a_5=150.06`.

`150.06=16r^(4)`

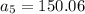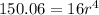
Divide both sides by 16.

`9.37875=r^(4)`

`(9.37875)^{(1)/(4)}=r`

`r\approx 1.75`

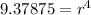
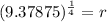
Substitute n=17,
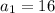`a_1=16` and
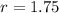`r=1.75` to find the 17th term.

`a_(17)=16(1.75)^(17-1)`

`a_(17)=123802.31384`

`a_(17)\approx 123802.31`

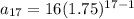
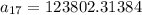
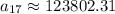
Therefore the correct option is 1.