Question

A chef is going to use a mixture of two brands of Italian dressing. The first brand contains 7% vinegar, and the second brand contains 12% vinegar. The chefwants to make 370 milliliters of a dressing that is 8% vinegar. How much of each brand should she use?

Answer 1

Assuming these are volume percentages and the volumes don't change when you mix them, we can calculate this using a system of equations.

But first we need to identify each equation and variable.

let x be the volume of 7% vinegar used and y be the volume of 12% vinegar used.

The total volume is the sum of those and it must be equal to 370 mL, so:

`x+y=370`

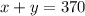
The amount of vinegar in the x volume of 7% vinegar can be calculated by multiplying x by the 7%, that is, by 0.07:

`0.07x`

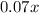
Similarly, the amount of vinegar in y is:

`0.12y`

So, the total amount of vinegar after the mixture is:

`0.07x+0.12y`

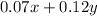
Since the percentage of the final mixture is 8%, the amount after the mixture can also be calculated by taking 8% of the final volume of 370mL, that is:

`0.08\cdot370=29.6`

The two ways of calculating the amount of vinegar in the mixture must be the same, so we have got our second equation:

`0.07x+0.12y=29.6`

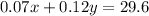
So, the system of equations is:

`\begin{gathered} x+y=370 \\ 0.07x+0.12=29.6 \end{gathered}`

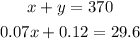
We can solve this by substitution:

`\begin{gathered} x+y=370 \\ x=370-y \end{gathered}`

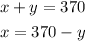
Thus:

`\begin{gathered} 0.07x+0.12y=29.6 \\ 0.07(370-y)+0.12y=29.6 \\ 0.07\cdot370-0.07y+0.12y=29.6 \\ 25.9+0.05y=29.6 \\ 0.05y=29.6-25.9 \\ 0.05y=3.7 \\ y=(3.7)/(0.05) \\ y=74 \end{gathered}`

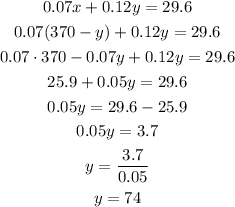
And, going back to the first equation:

`\begin{gathered} x=370-y \\ x=370-74 \\ x=296 \end{gathered}`