Answer:
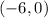
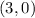
Explanation:
We have been given an quadratic function
 .
.
To find the x-intercept of he given function, we will equate our given function equal to zero.
Using zero product property we will get,
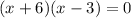
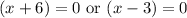
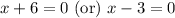
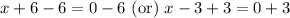
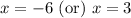
Since y-coordinate is zero at x-axis, therefore, the x-intercepts of our given function would be
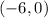 and
and
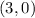 .
.