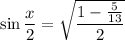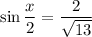Question

If cosx= 5/13 and sinx < 0 find sin(x/2)

Answer 1

Recall that


`\cos^2x+\sin^2x=1`

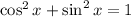
which means


`\sin^2x=1-\left(\frac5{13}\right)^2`

`\sin x=\pm\sqrt{(144)/(169)}=\pm(12)/(13)`

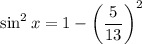
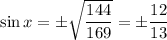
and since
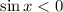
`\sin x<0` you take the negative root:


`\sin x=-(12)/(13)`

Now, you know that
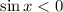
`\sin x<0` for
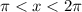
`\pi<x<2\pi` (third and fourth quadrants). In terms of
`\frac x2`, you have
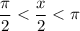
`\frac\pi2<\frac x2<\pi` (second quadrant). Over this interval, you have
`\sin\frac x2>0`.

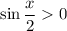
With this in mind, recall the half-angle identity for sine:


`\sin^2x=\frac{1-\cos2x}2`

`\sin x=\pm\sqrt{\frac{1-\cos2x}2}`

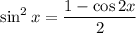
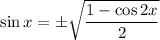
Replacing
`x` with
`\frac x2` gives


`\sin\frac x2=\pm\sqrt{\frac{1-\cos x}2}`

and using the fact that
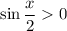
`\sin\frac x2>0`, you take the positive root.

Finally, you have


`\sin\frac x2=\sqrt{\frac{1-\frac5{13}}2}`

`\sin\frac x2=\frac2{√(13)}`