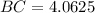Question

Create three different proportions that can be used to find BC in the figure above. At least one proportion must include AC as one of the measures.

Answer 1

We are given two similar triangles which are;

`\begin{gathered} \Delta AEB\text{ and }\Delta ADC \\ \end{gathered}`

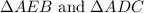
Note that the sides are not equal, but similar in the sense that the ratio of two sides in one triangle is equal to that of the two corresponding sides in the other triangle.

To calculate the length of side BC, we can use any of the following ratios (proportions);

`(AE)/(ED)=(AB)/(BC)`
`(AB)/(AC)=(AE)/(AD)`
`(AE)/(AB)=(AD)/(AC)`

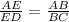
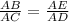
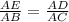
Using the first ratio as stated above, we shall have;

`\begin{gathered} (AE)/(ED)=(AB)/(BC) \\ (8)/(5)=(6.5)/(BC) \end{gathered}`

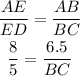
Next we cross multiply and we have;

`\begin{gathered} BC=(6.5*5)/(8) \\ BC=4.0625 \end{gathered}`

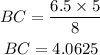
ANSWER:

`BC=4.0625`