we have the function
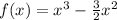
Find out the first derivative of the given function
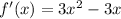
Equate to zero the first derivative

The values of x are
x=0 and x=1
we have the intervals
(-infinite,0) (0,1) (1,infinite)
Interval (-infinite,0) -----> f'(x) is positive
interval (0,1) ---------> f'(x) is negative
interval (1,infinite) -----> f'(x) is positive
that means
x=0 is a local maximum
x=1 is a local minimum
Find out the y-coordinates of the extreme values
For x=0 -----> substitute in the function f(x) ---------> f(x)=0
For x=1 ------> substitute in the function f(x) ------> f(x)=-0.5
therefore
The extreme values are
local maximum at (0,0)
local minimum at (1,-0.5)