Kelly is quite right that the denominator can not be zero. So let's not forget about that as we go through our steps.
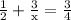
To get rid of the fractions let's multiply both sides of the equation by the Least Common Multiple of our denominators. We see a 2, 4 and x. The LCM of these values is 4x so we'll multiply both sides by 4x.
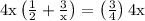
distribute the 4x to each term on the left,
and cancel stuff out as needed,
and do the same on the right side of the equation,
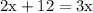
We've taken x out of the denominator though. So we should keep a note somewhere on the side of the page that x can not equal zero still. Even though we moved some things around, make our equation look different, we still have that restriction.

From this point, solve for x using Algebra:
Subtract 2x from each side,
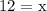
12 is a solution, and it is not 0.
If the solution had worked out to be x=0, we would reject it.