Question

Find the absolute extrema of the function. f(x) = xe^(-x^2) on [0 2]

Answer 1

`f(x)=xe^(-x^2)`

`f'(x)=(1-2x^2)e^(-x^2)`

`f''(x)=(4x^3-6x)e^(-x^2)`


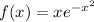
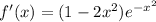
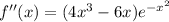
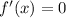
`f'(x)=0` whenever
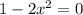
`1-2x^2=0`, which happens when
`x=\pm\frac1{\sqrt2}`. Only the positive root falls in the interval
`[0,2]`. At this point, you have
`f''\left(\frac1{\sqrt2}\right)<0` (concave downward). This indicates a maximum at
`\left(\frac1{\sqrt2},\frac1{√(2e)}\right)\approx0.7071,0.4289)`.

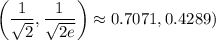
Meanwhile,
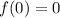
`f(0)=0` and
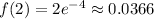
`f(2)=2e^(-4)\approx0.0366`, so the maximum above must be absolute, and the absolute minimum occurs at the origin.