
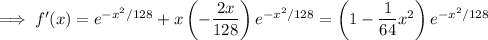
Extrema can occur when the derivative is zero or undefined.
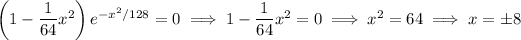
Maxima occur where the first derivative is zero and the second derivative is negative; minima where the second derivative is positive. You have
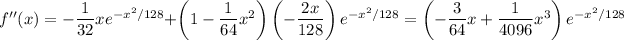
At the critical points, you get
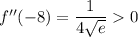
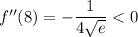
So you have a minimum at

and a maximum at
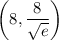
.
Meanwhile, as

, it's clear that
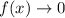
, so these extrema are absolute on the function's domain.