Question

Xe^(-x^2/128) absolute max and absolute min

Answer 1

`f(x)=xe^(-x^2/128)`

`\implies f'(x)=e^(-x^2/128)+x\left(-(2x)/(128)\right)e^(-x^2/128)=\left(1-\frac1{64}x^2\right)e^(-x^2/128)`

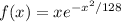
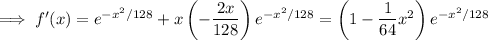
Extrema can occur when the derivative is zero or undefined.


`\left(1-\frac1{64}x^2\right)e^(-x^2/128)=0\implies 1-\frac1{64}x^2=0\implies x^2=64\implies x=\pm8`

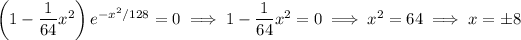
Maxima occur where the first derivative is zero and the second derivative is negative; minima where the second derivative is positive. You have


`f''(x)=-\frac1{32}xe^(-x^2/128)+\left(1-\frac1{64}x^2\right)\left(-(2x)/(128)\right)e^(-x^2/128)=\left(-\frac3{64}x+\frac1{4096}x^3\right)e^(-x^2/128)`

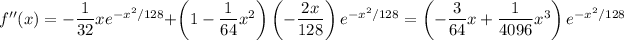
At the critical points, you get


`f''(-8)=\frac1{4\sqrt e}>0`

`f''(8)=-\frac1{4\sqrt e}<0`

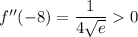
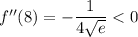
So you have a minimum at
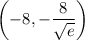
`\left(-8,-\frac8{\sqrt e}\right)` and a maximum at
`\left(8,\frac8{\sqrt e}\right)`.

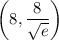
Meanwhile, as
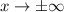
`x\to\pm\infty`, it's clear that
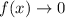
`f(x)\to0`, so these extrema are absolute on the function's domain.