Question

Given A= 25 B= 43 and C=17, solve triangle ABC. Round to the nearest hundredth.

Answer 1

I assume A, B and C are the side lengths
You can find the values of the angles using the cosine rule.

Answer 2

It is given that , In ΔABC , in which, ∠A=25°, ∠B=43°,

Length of side c= 17 units

As, angle sum property of triangle says that

∠A +∠B +∠C=180°

25°+43°+ ∠C=180°

∠C=180° -68°

∠C=112°

Using Sine Rule

`(a)/(Sin A^(\circ))=(b)/(Sin B^(\circ))=(c)/(Sin C^(\circ))\\\\ (a)/(Sin 25^(\circ))=(b)/(Sin 43^(\circ))=(17)/(Sin 112^(\circ))\\\\ a=(17 * Sin 25^(\circ))/(Sin 112^(\circ))\\\\a=(17 * 0.4226)/(0.9271)\\\\a=(7.1842)/(0.9271)\\\\a=7.749=7.75\\\\ b=(17 * Sin 43^(\circ))/(Sin 112^(\circ))\\\\b=(17 * 0.6819)/(0.9271)\\\\b=(11.5923)/(0.9271)\\\\b=12.5038=12.50`

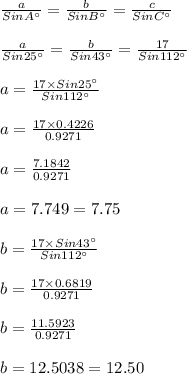
So, Side opposite to angle A=a=7.75 units

Side opposite to angle B=b=12.50 units

And , ∠C=112°