We know that Luke lost x pounds the first week.
We also know that the second week 3/2 less than 3/2 times the pounds he lost the first week, this means that the secons week he lost:
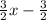
Finally the third week he lost 1 pound more than 3/4 of the pounds he lost the first week. This can be written as:
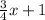
Hence luke lost a total of:
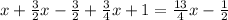
Therefore the expression for Luke's weight loss is:
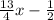
Liam lost the first week 1 pound less than 3/2 times the loss Luke had the first week this can be express as:
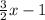
The second week he lost 4 pounds less than 5/2 times the loss of Luke the firs week then we have:
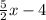
Finally Liam lost 1/2 pound more than 5/4 times the loss of Luke the first week, then:
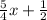
Adding this we have:
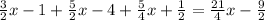
Therefore Liam's expression is:
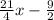
Now, we know that both of them lost the same weight, then we have the equation:
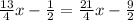
Solving for x we have:
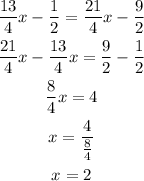
Therefore Luke lost 2 pound the first week.
Finally we plug the value of x in the expression for Luke's weight loss to get the total amount over the three weeks:
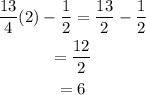
Therefore they lost 6 pounds in three weeks.