Question

What function is graphed below?

f(x) = log (x − 3)
f(x) = log (x + 3)
f(x) = log x + 3
f(x) = log x − 3

Answer 1

Because the graph is shifted up three units from the original mother function (f(x) = log x), and therefore, the answer is f(x) = log x + 3. 

Answer 2

The function that is graphed is:

`f(x)=\log x+3`

Explanation:

We could clearly observe from the graph that:

when x=1 we have the value of the function as: f(1)=3

This means that from the given options we will check which option satisfies this property.

1)

`f(x)=\log (x-3)`

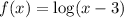
when x=1 we have:

`f(1)=\log 1-3)\\\\f(1)=\log (-2)`

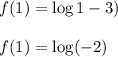
As we know that the logarithmic function is not defined for the negative value.

Hence, this option is incorrect.

2)

`f(x)=\log (x+3)`

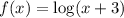
when x=1 we have:

`f(2)=\log (1+3)\\\\f(2)=\log (4)=0.6040`

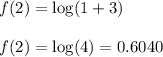
Hence, this option is incorrect.

4)

`f(x)=\log x-3`

when x=1 we have:

`f(1)=\log 1-3\\\\f(1)=0-3\\\\f(1)=-3`

Hence, this option is incorrect.

3)

`f(x)=\log x+3`

When we plot this function we get the same graph as shown.

Also f(1)=3

Hence, this option is correct.