Question

A man on the fifth floor of a building shouts down to a person on the street. If the angle of elevation from the street to the man in the building is 35° and the man in the building is 40 feet up, about how far away from the building is the person on the street?

Answer 1

The answer is about 57 feet.

Answer 2

Answer: 57 feet

Explanation:

Given: The angle of elevation from the street to the man in the building=
`35^(\circ)`

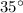
If the man in the building is 40 feet up.

From the given , we make a diagram in which
`\triangle {ABC}` is a right triangle, such that

Let AB=40 feet

Then
`\tan{35^(\circ)}=(AB)/(BC)`

`\\\Rightarrow0.70=(40)/(BC)\\\\\Rightarrow\ BC=(BC)/(0.70)=57.142\approx57\ feet`

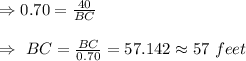
Hence, the distance of the person on the street from the building is 57 feet