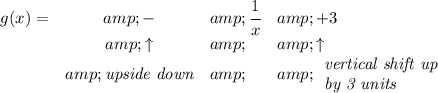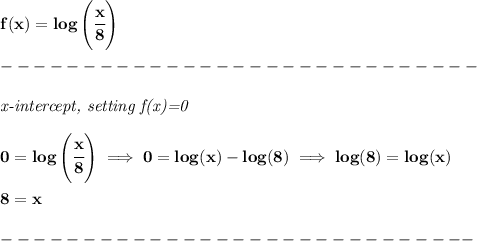
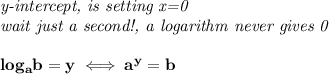
p, li { white-space: pre-wrap; }
----------------------------------------------------------------------------------------------
now on 2)
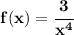if the denominator has a higher degree than the numerator, the horizontal asymptote is y = 0, or the x-axis,
in this case, the numerator has a degree of 0, the denominator has 4, thus y = 0
vertical asymptotes occur when the denominator is 0, that is, when the fraction becomes undefined, and for this one, that occurs at
or the y-axis
----------------------------------------------------------------------------------------------
now on 3)
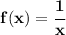
now, let's see some transformations templates
![\bf \qquad \qquad \qquad \qquad \textit{function transformations} \\ \quad \\ \begin{array}{rllll} % left side templates f(x)=&{{ A}}({{ B}}x+{{ C}})+{{ D}} \\ \quad \\ y=&{{ A}}({{ B}}x+{{ C}})+{{ D}} \\ \quad \\ f(x)=&{{ A}}\sqrt{{{ B}}x+{{ C}}}+{{ D}} \\ \quad \\ f(x)=&{{ A}}\mathbb{R}^{{{ B}}x+{{ C}}}+{{ D}} \end{array}]()
![\bf \begin{array}{llll} % right side info \bullet \textit{ stretches or shrinks horizontally by } {{ A}}\cdot {{ B}}\\ \bullet \textit{ horizontal shift by }\frac{{{ C}}}{{{ B}}}\\ \qquad if\ \frac{{{ C}}}{{{ B}}}\textit{ is negative, to the right}\\ \qquad if\ \frac{{{ C}}}{{{ B}}}\textit{ is positive, to the left}\\ \bullet \textit{ vertical shift by }{{ D}}\\ \qquad if\ {{ D}}\textit{ is negative, downwards}\\ \qquad if\ {{ D}}\textit{ is positive, upwards} \end{array}]()
now, let's take a peek at g(x)
