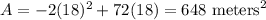Question

An enclosed area is designed using one existing wall, and 72m of fence material. What is the maximum area of the enclosure?

Answer 1

The maximum area possible is 648 squared meters.

Explanation:

Let the length of the existing wall be
`\ell`.

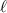And let the width of the fence be
`w`.

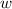The area of the enclosure will be given by:

`A=w\ell`

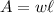
Since the area is bounded by one existing wall, the perimeter (the 72 meters of fencing material) will only be:

`72=2w+\ell`

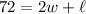
We want to maximize the area.

From the perimeter, we can subtract 2w from both sides to obtain:

`\ell=72-2w`

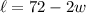
Substituting this for our area formula, we acquire:

`A=w(72-2w)`

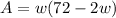
This is now a quadratic. Recall that the maximum value of a quadratic always occurs at its vertex.

We can distribute:

`A=-2w^2+72w`

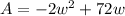
Find the vertex of the quadratic. Using the vertex formula, we acquire that:

`\displaystyle w=-(b)/(2a)=-((72))/(2(-2))=18`

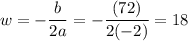
So, the maximum area is:

`A=-2(18)^2+72(18)=648\text{ meters}^2`