1 Answer

Ask a Question

Thiago Melo · Answer 1 · 2023-10-18T01:27:31+0000

Answer:

Tangent to radius of a circle theorem

A tangent to a circle forms a right angle with the circle's radius, at the point of contact of the tangent.

Part A:

With the theorem above, we will have that the tangent is perpendicular to the line radius drawn from the point of tangency

Therefore,

The value of angle CBA will be

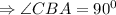
$\Rightarrow\angle CBA=90^0$

Part B:

Since the angle formed between the tangent and the radius from the point of tangency is 90°

Hence,

The final amswer is

Tangent lines are PERPENDICULAR to a radius drawn from the point of tangency

Part C:

Concept:

Three interior angles of a triangle will always have the sum of 180°

Hence,

The measure of angles in a triangle will add up to give

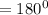
Part D:

Since we have the sum of angles in a triangle as

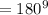
Then the formula below will be used to calculate the value of angle BCA

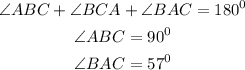
$\begin{gathered} \angle ABC+\angle BCA+\angle BAC=180^0 \\ \angle ABC=90^0 \\ \angle BAC=57^0 \end{gathered}$

By substituting the values,we will have

$\begin{gathered} \operatorname{\angle}ABC+\operatorname{\angle}BCA+\operatorname{\angle}BAC=180^(0) \\ 90^0+57^0+\operatorname{\angle}BCA=180^0 \\ 147^0+\operatorname{\angle}BCA=180^0 \\ substract\text{ 147 from both sides} \\ 147^0-147^0+\operatorname{\angle}BCA=180^0-147^0 \\ \operatorname{\angle}BCA=33^0 \end{gathered}$

Hence,

The measure of ∠BCA = 33°

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions