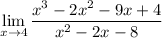
First notice that
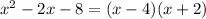
. If

is not a factor of the numerator, then there is a non-removable discontinuity at
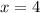
, and a removable discontinuity otherwise.
You have
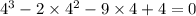
, which means, by the polynomial remainder theorem, that

is indeed a linear factor of the numerator. Dividing yields a quotient of
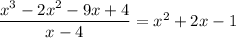
so the limit is
