Question

A parabola has a vertex at (-1, 0) and opens down. What is the equation of the parabola?

y = -x^2 - 1
y = -(x - 1)^2
y = -(x + 1)^2

Answer 1

vertex form

for

y=a(x-h)^2+k
vertex is (h,k)
and if a is poisitve it opens up and if it is negative it opens down

so it is opening down and has vertex at (-1,0)

y=-(x-(-1))^2+0
y=-(x+1)^2

last option

Answer 2

C.
`-(x+1)^2`

Explanation:

We have been given that a parabola has a vertex at (-1, 0) and opens down. We are asked to find the equation of the parabola.

We know that the vertex form of parabola is in form:
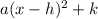`a(x-h)^2+k`, where, point (h,k) is the vertex of parabola and sign of 'a' determines whether parabola opens upwards and downwards.

Since the vertex of our given parabola is at (-1,0) and it opens downwards, so the leading coefficient will be negative.

`-(x--1)^2+0`

`-(x+1)^2`

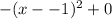
Therefore, the equation of the parabola is
`-(x+1)^2` and option C is the correct choice.