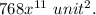Question

A rectangular pasture has a fence around the perimeter. The length of the fence is 16x^7 and the width is 48x^4. What is the area of the pasture?

Answer 1

A=LW
multily
remmber

`(x^m)(x^n)=x^(m+n)`
so

`(16x^7)(48x^4)=(16)(x^7)(48)(x^4)=`
`(16)(48)(x^7)(x^4)(768)(x^(7+4))=768x^(11)`

Answer 2

The area of the rectangular pasture is
`768x^(11)\ unit^(2).`

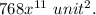
Explanation:

Formula

Area of a rectangle = Length × Breadth

As given

A rectangular pasture has a fence around the perimeter. The length of the fence is
`16x^(7)` and the width is
`48x^(4)`.

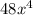Put all the values in the formula

`Area\ of\ a\ rectangular\ pasture = 16x^(7)* 48x^(4)`

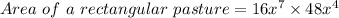
Now by using the exponent

`x^(a)* x^(b) = x^(a+b)`

`Area\ of\ a\ rectangular\ pasture = 16* 48* (x^(7+4))`

`Area\ of\ a\ rectangular\ pasture = 768(x^(11))`

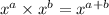
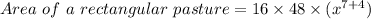
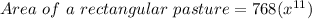
Therefore the area of the rectangular pasture is
`768x^(11)\ unit^(2).`