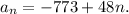Question

Find an equation for the nth term of the arithmetic sequence.

a15 = -53, a16 = -5

Answer 1

48n-773 is the equation for the nth term

Answer 2

Answer: The required equation for the n-th term is
`a_n=-773+48n.`

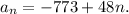
Step-by-step explanation: We are given to find the equation for the nth term of the arithmetic sequence with the fifteenth and sixteenth term as follows :

`a_(15)=-53,~~~a_(16)=-5.`

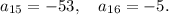
We know that

the nth term of an arithmetic sequence with first term a and common difference d is given by

`a_n=a+(n-1)d.`

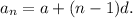
So, we have

`a_(15)=-53\\\\\Rightarrow a+(15-1)d=-53\\\\\Rightarrow a+14d=-53~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

and

`a_(16)=-5\\\\\Rightarrow a+(16-1)d=-5\\\\\Rightarrow a+15d=-5~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

Subtracting equation (i) from equation (ii), we get

`(a+15d)+(a+14d)=-5-(-53)\\\\\Rightarrow d=48.`

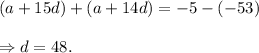
And, from equation (i), we get

`a+14*48=-53\\\\\Rightarrow a+672-53\\\\\Rightarrow a=-725.`

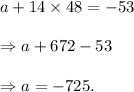
Therefore, the n-th term of the given sequence is

`a_n=a+(n-1)d\\\\\Rightarrow a_n=-725+(n-1)48\\\\\Rightarrow a_n=-773+48n.`

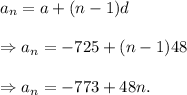
Thus, the required equation for the n-th term is
`a_n=-773+48n.`