Question

Solve the following quadratic equation using the quadratic formula and then choose the correct solution set.

8x2 - 6x + 1 = 0

{1/8,5/8 }
{1/4, 1/2}
{±1/2}

Answer 1

8x2 - 6x + 1 = 0
(2x-1)(4x-1) = 0

2x-1 = 0
x=1/2

4x-1=0
x = 1/4

answer {1/4, 1/2}(second choice)

Answer 2

Answer: The the correct solution set is (B)
`\{(1)/(4),(1)/(2)\}.`

Step-by-step explanation: The given equation is

`8x^2-6x+1=0.~~~~~~~~~~~~~~(i)`

We are to choose the correct solution set after solving the above equation by using quadratic formula.

We know that, the solution set for the quadratic equation
`ax^2+bx+c=0,~a\\eq 0` is given by

`x=(-b\pm √(b^2-4ac))/(2a).`

In the given equation (i), we have

`a=8,~~b=-6,~~c=1.`

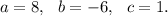
Therefore, the solution set will be given by

`x=(-b\pm √(b^2-4ac))/(2a)\\\\\\\Rightarrow x=(-(-6)\pm √((-6)^2-4* 8* 1))/(2* 8)\\\\\\\Rightarrow x=(6\pm√(36-32))/(16)\\\\\\\Rightarrow x=(6\pm√(4))/(16)\\\\\\\Rightarrow x=(6\pm 2)/(16)\\\\\\\Rightarrow x=(6+2)/(16),~~(6-2)/(16)\\\\\\\Rightarrow x=(8)/(16),~~(4)/(16)\\\\\\\Rightarrow x=(1)/(2),~~(1)/(4).`

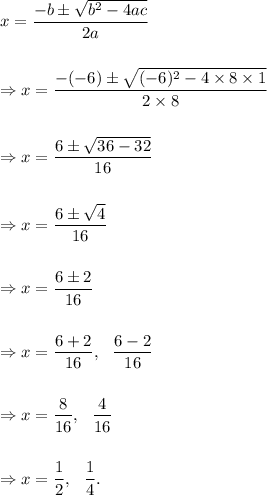
Thus, the correct solution set is (B)
`\{(1)/(4),(1)/(2)\}.`