Question

Find the sum of the first 39 terms of the following series, to the nearest integer.2,7, 12,...

Answer 1

The sequence 2,7,12,... given is an arithmetic progression. This is because it has a common difference.

Given:

first term, a = 2

common difference, d = second term - first term = 7 - 2 = 5

d = 5

n = 38

The sum of an arithmetic progression is given by;

`\begin{gathered} S_n=(n)/(2)\lbrack2a+(n-1)d\rbrack \\ S_(38)=(38)/(2)\lbrack2(2)+(38-1)5\rbrack \\ S_(38)=19\lbrack4+37(5)\rbrack \\ S_(38)=19\lbrack4+185\rbrack \\ S_(38)=19(189) \\ S_(38)=3591 \end{gathered}`

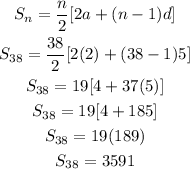
Therefore, the sum of the first 39 terms of the series is 3,591