Question

How many and what type of solution(s) does the equation have?6p2 = 8p + 32 rational solutions1 rational solutionNo real solutions2 irrational solutions

Answer 1

We are going to solve the question using the quadratic formula

`\begin{gathered} x=\frac{-b\pm\sqrt[]{(b^2}-4ac)}{2a} \\ \text{where the quadratic equation is ax}^2+bx+c=0 \end{gathered}`

The quadratic equation given is

`\begin{gathered} 6p^2=8p+3 \\ 6p^2-8p-3=0 \\ \text{where a=6} \\ b=-8 \\ c=-3 \end{gathered}`

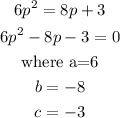
By substitution we will have,

`\begin{gathered} p=\frac{-(-8)\pm\sqrt[]{(-8)^2}-(4*6*-3)}{2*6} \\ p=\frac{8\pm\sqrt[]{64+72}}{12} \\ p=\frac{8\pm\sqrt[]{136}}{12} \\ p=\frac{8\pm\sqrt[]{4*34}}{12} \\ p=\frac{8\pm2\sqrt[]{34}}{12} \\ p=\frac{2(4\pm\sqrt[]{34)}}{12} \\ p=\frac{4\pm\sqrt[]{34}}{6} \\ p=\frac{4+\sqrt[]{34}}{6}\text{ or p=}\frac{4-\sqrt[]{34}}{6} \end{gathered}`

Therefore,

With the roots gotten from the quadratic equation, we can therefore deduce that the solutions to the equation 6p²=8p+3 will give 2 irrational roots.

The correct answer is OPTION D