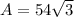Question

Find the area of a regular hexagon with the given measurement. 6-inch radius

Answer 1

`54√(3)`

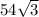
Explanation:

In order to solve a regular polygon, you would use the equation:
`A=(1)/(2) (a)(p)`

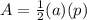
First start by replacing the variables in that equation with what we know. We know that the radius is 6 inches and that hexagons are made up of equilateral triangles. If a 6 inch radius is the side of a single equilateral triangle, then all the sides on that triangle = 6. If all the sides on that one triangle = 6, then all the sides on all the triangles = 6. Therefore, each side of the hexagon = 6.

Now we know that the perimeter = 36. Now our equation is
`A=(1)/(2) (a)(36)`.

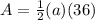The apothem is
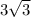`3√(3)` because the apothem, side, and radius create a right triangle. We know that the radius and side = 6, and if the apothem divides the side in half then the short leg of our triangle = 3. If the length of hypotenuse of our right triangle = 6 and the length of the short leg = 3, then we can use Pythagorean theorem to find the long leg aka. the apothem.

Our equation would then be
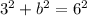`3^(2) +b^(2) =6^(2)` and so
`b=3√(3)`.

Now we know what our apothem is so our equation is now
`A=(1)/(2) (3√(3) )(36)`

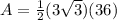
Therefore
`A=54√(3)`

Answer 2

 It would probably be 93.5. I hope this helps. have a blessed day.