Question

A 4000-kg truck traveling with a velocity of 20 m/s due south collides head-on with a 1320- kg car traveling with a velocity of 10 m/s due north. The two vehicles stick together after the collision.A. What are the magnitude and the direction of the momentum of each vehicles Prior to the collision?B. What are the magnitude and the direction of the velocity of both vehicles after their collide?

Answer 1

Before we begin, we will establish that the north direction is the positive direction which means that the south direction is negative.

A.

The momentum of an object is given by:

`p=mv`

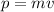
For the truck we know that the velocity is -20 m/s (since it is traveling south) and its mass is 4000 kg, then its momentum is:

`p=(4000)(-20)=-80000`

Therefore, the momentum of the truck is -80000 kg m/s; this means that its magnitude is 80000 kg m/s and its direction is south.

For the car we know that the velocity is 10 m/s and its mass is 1320 kg, then its momentum is:

`p=(1320)(10)=13200`

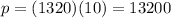
Therefore, the momentum of the car is 13200 kg m/s which means that its magnitude is 13200 kg m/s and its direction is north.

B.

In a collision the momentum is conserved, that is, the total initial and final momentum is equal, that is:

`p_i=p_f`

In this case, we know that the vehicles stick together after they collide, then we have:

`m_tv_t+m_cv_c=(m_t+m_c)u`

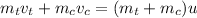
where u is the velocity of the vehicles after they collide. Plugging the values we know, we have that:

`\begin{gathered} -80000+13200=(4000+1320)u \\ u=(-80000+13200)/(4000+1320) \\ u=-12.56 \end{gathered}`

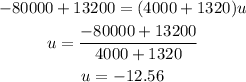
Therefore, the final velocity of the system is -12.56 m/s which means that the magnitude of the velocity is 12.56 m/s and its direction is south.