
Recall that the cosine of the angle between the vectors is given by,

So we have a bunch of things we need to do.
Find the dot product of u and v,
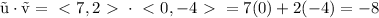
That gives us our numerator,
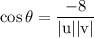
Find the magnitude of each vector,

Ok that gives us our denominator,
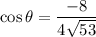
To find your angle theta, apply inverse cosine,

Let your calculator do the rest.
Hope that helps!