The given triangle has vertices at:
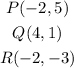
In the coordinate plane, the triangle looks like this:
There are different forms to find the circumcenter, we are going to use the midpoint formula:
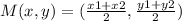
Apply this formula for each vertice and find the midpoint:
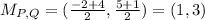
For QR:
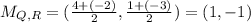
For PR:
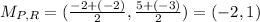
Now, we need to find the slope for any of the line segments, for example, PQ:
We can apply the slope formula:
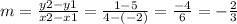
By using the midpoint and the slope of the perpendicular line, find out the equation of the perpendicular bisector line, The slope of the perpendicular line is given by the formula:
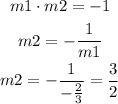
The slope-intercept form of the equation is y=mx+b. Replace the slope of the perpendicular bisector and the coordinates of the midpoint to find b:
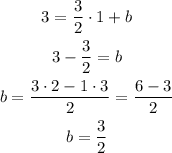
Thus, the equation of the perpendicular bisector of PQ is:
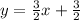
If we graph this bisector over the triangle we obtain:
Now, let's find the slope of the line segment QR:
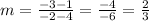
The slope of the perpendicular bisector is:
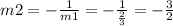
Let's find the slope-intercept equation of this bisector:
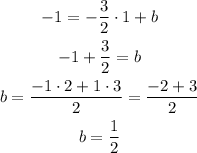
Thus, the equation is:
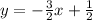
This bisector in the graph looks like this:
Now, to find the circumcenter we have to equal both equations, and solve for x:

Now replace x in one of the equations and solve for y:
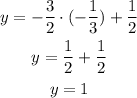
The coordinates of the circumcenter are: (-1/3,1).
In the graph it is: