Question

Determine the values of the constants B and C so that the function given below is differentiable.

f(x)= {8x^3, x less than equal to 1
        {Bx+C, x > 1

Answer 1

For the function to be differentiable, its derivative has to exist everywhere, which means the derivative itself must be continuous. Differentiating gives


`f'(x)=\begin{cases}24x^2&\text{for }x<1\\?&\text{for }x=1\\B&\text{for }x>1\end{cases}`

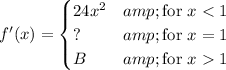
The question mark is a placeholder, and if the derivative is to be continuous, then the question mark will have the same value as the limit as
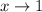
`x\to1` from either side.


`\displaystyle\lim_(x\to1^-)f'(x)=\lim_(x\to1)24x^2=24`

`\displaystyle\lim_(x\to1^+)f'(x)=\lim_(x\to1)B=B`

So the derivative will be continuous as long as
`B=24`

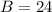
For the function to be differentiable everywhere, we need to require that
`f(x)` is itself continuous, which means the following limits should be the same:


`\displaystyle\lim_(x\to1^-)f(x)=\lim_(x\to1)8x^3=8`

`\displaystyle\lim_(x\to1^+)f(x)=\lim_(x\to1)Bx+C=24+C`


`24+C=8\implies C=-16`

So, the function should be


`f(x)=\begin{cases}8x^3&\text{for }x\le1\\24x-16&\text{for }x>1\end{cases}`

with derivative


`f'(x)=\begin{cases}24x^2&\text{for }x<1\\24&\text{for }x\ge1\end{cases}`