Question

Lim as x goes to 0:

(2sinxcosx)/2x

I'm pretty sure I have it right (answer being 1) but i'd like an explanation to compare to my own. Thanks!

Answer 1

They want you to make use of this limit identity:


`\rm \lim\limits_(t\to0)(sin(t))/(t)=1`

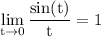
y=sin(x) and y=x approach zero at the same rate.

So with your problem you simply apply your Sine Double Angle Identity,


`\rm \lim\limits_(x\to0)(2sin x cos x)/(2x)=\lim\limits_(x\to0)(sin(2x))/(2x)`

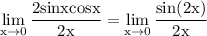
From this point, hopefully you can see that we have our identity with t=2x. So yes, you are correct :) the result is 1.