Question

Object a attracts objects be the gravitational force of 10 N from a given distance the distance between the two objects is doubled what is the new force of attraction between

Answer 1

We are given that two objects are being attracted by a gravitational force between each other of 10N. The gravitational force between two masses is given by the following equation:

`F_g=G(m_Am_B)/(r^2)`

Where:

`\begin{gathered} F_g=\text{ Gravitational force} \\ m=\text{mass} \\ G=\text{ Gravitational constant} \\ r=\text{ distance between the masses} \end{gathered}`

Replacing the given values for the 10N force:

`10=G(m_Am_B)/(r^2_1)`

Where:

`r_1=\text{ initial distance}`

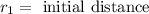
Now we will solve for the product of the masses and the gravitational constant by multiplying both sides by the distance squared:

`10r^2_1=Gm_Am_B`

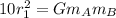
Now, the product of the masses and the gravitational constant won't change if we double the distance, therefore, if we apply the equation for the gravitational force for the new distance we get:

`F_(g2)=G(m_Am_B)/(r^2_2)`

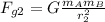
We can replace the value we determined earlier:

`F_(g2)=(10r^2_1)/(r^2_2)`

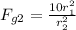
Since the distance is double, we have:

`r_2=2r_1`

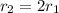
Replacing in the previous equation:

`F_(g2)=(10r^2_1)/((2r_1)^2)`

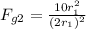
Solving the square:

`F_(g2)=(10r^2_1)/(4r^2_1)`

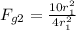
Now we can cancel out the distances squared:

`F_(g2)=(10)/(4)`

Solving the operation:

`F_(g2)=2.5`

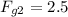
Therefore, doubling the distance the new gravitational force is 2.5N.