Question

The shape of Sugarloaf mountain, in Rio de Janeiro, Brazil, is such that, if you

were to kick a soccer ball hard enough, it could land near the base of the mountain
without hitting the mountain's side. Suppose the ball is kicked horizontally with an
initial speed of 9:37 m/s. If the ball travels a horizontal distance of 85.0 m, how tall
is the mountain?

Answer 1

The mountain is 403 m tall

Step-by-step explanation:

Horizontal Launch

When an object is thrown horizontally with a speed v from a height h, it describes a curved path ruled by gravity until it hits the ground.

The range or maximum horizontal distance traveled by the object can be calculated as follows:

`\displaystyle d=v\cdot\sqrt{\frac {2h}{g}}`

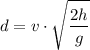
It's given that if a ball is kicked from the top of the Sugarloaf Mountain, it will land near its base without hitting the side. The initial speed is v=9.37 m/s and it reaches a horizontal distance of d=85 m. Solving the equation for h:

`\displaystyle h=(d^2g)/(2v^2)`

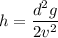
Substituting:

`\displaystyle h=(85^2*9.8)/(2*9.37^2)`

`\displaystyle h=403 \ m`

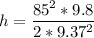
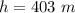
The mountain is 403 m tall