Question

I need help with this practice problem If you can, show your work step by step so I can take helpful notes

Answer 1

The given geometric series is

`120-80+(160)/(3)-(320)/(9)+\cdots`

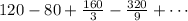
In a geometric series, there is a common ratio between consecutive terms defined as

`r=\frac{-80_{}}{120_{}}=-(2)/(3)`

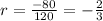
The sum of the first n terms of a geometric series is given by

`S_n=(a(1-r^n))/(1-r),r<1`

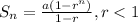
Where a is the first term.

From the given series

a = 120

Hence, the sum of the first 8 terms is

`S_8=(120(1-(-(2)/(3))^8))/(1-(-(2)/(3)))`

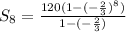
Simplify the brackets

`S_8=\frac{120(1-(2^8)/(3^8)^{})}{1+(2)/(3)}`

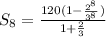
Simplify further

`\begin{gathered} S_8=(120(1-(256)/(6561)))/((3+2)/(3)) \\ S_8=(120((6561-256)/(6561)))/((5)/(3)) \\ S_8=(120((6305)/(6561)))/((5)/(3)) \\ S_8=(120*6305)/(6561)/(5)/(3) \\ S_8=(120*6305)/(6561)*(3)/(5) \\ S_8=(120*6305)/(6561)*(3)/(5) \\ S_8=(8*6305)/(729) \\ S_8=(50440)/(729) \end{gathered}`

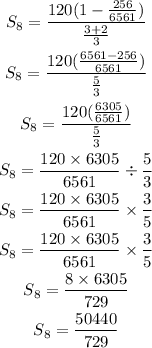
Therefore, the sum of the first 8 terms is

`(50440)/(729)`